Now we begin introducing a discursive criterion, and after, will continue with a rigorous definition. First of all, we can highlight a characteristic that distinguishes unextended from extended ones: the first are homogeneous, the second are heterogeneous, because extended ones possess overall qualities independent of their content.
Let's start with some examples of unextended ones.
The number 2 is unextended idea, abstract, with no height, width or depth, and in fact it is homogeneous: it can only refer to objects that participate idea of 2, such two apples, two oranges, two eyes, but not to a single eye or a single apple, because they don’t participate the idea of 2.
Justice is unextended idea, abstract, with no height, width or depth, and in fact it is homogeneous: it can only refer to objects that participate the idea of justice, that is, policemen, judges, heroes and so on, but not an apple or a leg, because apples and legs have nothing to do with idea of justice.
Let’s start now with extended ones.
Triangle is extended, with height and width, and heterogeneous: contains points, sides or a circle inscribed in, but overall it can refer to qualities that have nothing to do with elements contained within. In fact, triangle can refer to Egyptian pyramids, road signs, love affairs, and many other concepts that are relevant to overall idea of a triangle but not to elements contained within.
A human being is extended, with height, width and depth, and heterogeneous: contains protons, neutrons and electrons, but overall it can refer to qualities that have nothing to do with elements contained within. It can refer to beauty, intelligence, ability to love, nourish and many other concepts that are relevant to overall idea of human being but not to elements contained within.
A typical example about difference between unextended and extended objects is difference between beauty and Miss America.
Beauty is unextended and homogeneous: it can only refer to concepts that participate the idea of beauty, such harmony, youth, competitions, dances, and so on, but not to dental fillings, because they have nothing to do with idea of beauty. Opposite to beauty, Miss America is extended and heterogeneous: she contains bones, muscles and dental fillings, but overall it can refer to concepts of humanity and beauty.
Another interesting example is difference between sunset and atmosphere.
Sunset is unextended and homogeneous: it can only refer to objects that participate the idea of sunset, as the Sun, clouds, landscape and the horizon, but not hydrogen and nitrogen, because they have nothing to do with idea of sunset. Opposite to sunset, atmosphere is extended and heterogeneous: it contains hydrogen and nitrogen, however can refer to Sun, clouds, landscape, the horizon and all those concepts that are relevant to overall idea of atmosphere.
Through all these examples the extended objects results ambivalent, because they have overall elements extraneous to their content.
How can we logically describe this concept?
First of all, let's start by defining what means "overall".
An object can be defined through a series of "or" conditions, that is logical disjunctions, to define its different manner, and its overall vision corresponds to a series of "and" conditions, that is logical conjunctions, where indissolubly binds manner together, in a single whole. Eg:
C = H or T
N(C) = N(H) and N(T)
This means coin tosses, "C", returns heads or tails, "H or T", however the set of all tosses, "N(C)", corresponds to the tosses that give heads, plus tails, “N(H) and N(T)”.
The function N(x) means "grouping of x", or "set of x", and is necessary otherwise the logical conjunction would return the empty set, since the single options are alternatives to each other, that is: " H and T = empty set ".
The function N(x) does not refer to a specific multiplicity, it is not certain that the single objects must be more than one. In the previous example, the coin tosses can be infinite, but in other cases the multiplicity is only one. In the next example we see a hand can be the right or the left, so the set of all hands is given by the right plus the left, with the multiplicities that are respectively two, one and one.
hand = right or left
N(hand) = N(right) and N(left)
Furthermore, the "and" conditions requires the objects inextricably linked in the overall ensemble, so that, by eliminating a single option, the whole set is invalid.
For example, a single hand can be the right, and not the left, but the overall set must necessarily contain both the right and the left. Similarly, the set of coin tosses must contain both tosses that give heads and those that give tails, even if, by chance, one of the two cases never occurs. Previous two examples referred to unextended objects, with no height, width or depth. Coin tosses are unextended events, because they are a concept with no space extent. In the same way, set of hands is unextended, because has no height, width or depth, although their single members, hands, are extended. In fact, you can see that an unextended object, such a set, can be composite by extended members: look at the set of the horses, is unextended, when the horses are extended.
Let us now turn to extended objects.
We said extended objects are ambivalent, because they have overall parts that are extraneous to their content. This concept can be explained by next two expressions:
A = B1 or B2 or… or Bn
N(A) = N(B1) and N(B2) and … and N(Bn) and X
In the first expression we can see the component A in "n" different ways, as we have previously seen in the case of coin tosses or hands. In the second expression, we see the set of these elements, N(A), containing an extraneous/overall part "X", that is not related to elements of first expression, and appears only in logical conjunction. In other words, extended objects involve the breaking of the one-to-one correspondence between elements in logical disjunction and logical conjunction, which instead characterized unextended objects, with the addition of an extraneous element "X" in the logical conjunction.
Let's see some examples.
The next image depicts a square.
The square can be described by the next two expressions:
T = T1 or T2 or T3 or T4
Square = N(T) = N(T1) and N(T2) and N(T3) and N(T4) and X
The first expression means that the generic T element that composes the square can be the triangle T1 or T2 or T3 or T4. The second expression means that the square, in addition to containing the set of T elements, must have an X component, extraneous/overall to the individual elements, that could specifically indicate:
X = "has all sides equal", otherwise it would not be a square.
X is a property of N(T), just like the individual N(Tj).
Instead of X = "has all sides equal", we can write X = "has the elements one below the other", or X = "has the elements next to each other", and still we have extended in space objects, even if no squares, as you can see in the next picture. Only the lack of X makes the unextended object, with no height, width or depth, reducing it to an abstract list of triangles, without space extent.

Let's see other examples of extended in space objects.
Look at the next picture, corresponding to a cabinet with two drawers and the base.
The cabinet can be described using the next two expressions:
C = a1 or … or an or b1 or … or bn or c1 or … or cn
Cabinet = N(C) = N(aj) and N(bj) and N(cj) and X
The first expression will means that the generic C element of the cabinet is a generic aj member of the first drawer, or a generic bj member of the second drawer, or a generic cj member of the base. The second expression means that the cabinet, in addition to containing the set of the two drawers and the base, has an X component, extraneous/overall to individual elements, to indicate that the two drawers and the base are placed one under the other, X = "one under the other". Otherwise the drawers and the base would not be connected in space extent.
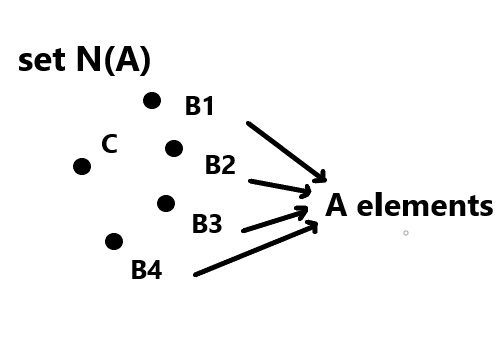
Look at the next picture, corresponding to set of points B1, B2, B3 and B4.
Set of points B1, B2, B3, B4 can be described by next two expressions:
A = B1 or B2 or B3 or B4
N(A) = N(B1) and N(B2) and N(B3) and N(B4) and X
The first expression means that the generic point A is equal to B1 or B2 or B3 or B4. The second expression means that N(A), set of those points, in addition to have the Bn individual points, must have an X element, extraneous/overall to individual, to indicate X = "equidistant from C point”, otherwise it would be abstract, not a material set of points extended on a plane.
Instead of write X = "equidistant from C point”, we can write X = "equidistant from each other", and still we have a set of points extended in space. Only the lack of X makes an unextended set, without space extent.
The next examples are specifically about Mathematics.
A set of numbers, finite or infinite, is unextended in space, with no height, width or depth, and we can write it as:
I = {1, 2, 3, 4 ,… }
With our methodology, we can rewrite the set using the next two expressions:
n = 1 or 2 or 3 or 4 or …
N(n) = N(1) and N(2) and N(3) and N(4) and …
The first expression means that the generic element “n” is equal to 1 or 2 or 3 or 4 and so on. The second expression means that the set of those numbers is equal to 1 and 2 and 3 and 4 and so on. Now let's try to add an X element in logical conjunction, extraneous/overall to elements, such as X = "increasing order":
N (n) = N (1) and N (2) and N (3) and N (4) and… and X.
Well, we see that adding extraneous/overall X="increasing order", the unextended set becomes extended in space, because “increasing order” means a straight line, a thermometer, a clock, which are all extended in space objects. In fact, the increasing order leads a position from bottom to top, or left to right, which are concepts inherent the space extent.
Let's see the next example.
“P” point in the “n” dimensional Cartesian space can be written as P = (x1, x2, x3,…, xn).
With our methodology, that point can be described by next two expressions:
r = x1 or x2 or x3 or … or xn
P = N(r) = N(x1) and N(x2) and N(x3) and … and N(xn) and X
The first identifies a generic real number "r", equal to x1 or x2 or x3 or… or xn. The second identifies “P” point, having in addition to real numbers an X element extraneous/overall to individual numbers, to indicate "numbers are coordinates", otherwise P would be only an abstract list of "n" real numbers. This X element characterizes P extended in space, such as the mathematical functions. Otherwise, the lack of X, reduce P to an unextended list of numbers.
Finally, we will conclude this paragraph giving one of the previous examples:
difference between beauty, unextended in space, and Miss America, extended in space.
Beauty can be described by next two expressions:
example = harmony or youth or seduction
Beauty = N(example) = N(harmony) and N(youth) and N(seduction)
The first expression identifies a single example of beauty, equal to harmony, youth or seduction. The second expression defines beauty as the set of these singular examples, where the "or" elements are in perfect one-to-one correspondence with the "and" elements, without X extraneous/overall parts.
Opposite to beauty, Miss America can be described using next two expressions:
Element = bone or muscle or dental filling
Miss America = N(Element) = N(bone) and N(muscle) and N(dental filling) and X
The first expression identifies the generic component of Miss America as a bone, a muscle or a dental filling. The second expression identifies Miss America, having in addition to singular elements, an X component, extraneous/overall to singular elements, that means the beauty, harmony and seduction, to characterize whole set “Miss America” extended in space.
Three-dimensional Venn diagrams
The previous two paragraphs lead us to imagine concepts as two-faced objects. Each object has two faces: it can be a single element or a whole, depending on choose "or" or "and" operator. As you can see in the next picture, the metaphorical representation of an object is a three-dimensional Venn diagram. One of the two orthographic projections corresponds to "or" view, where the components are mutually exclusive and their intersection returns the empty set. The other orthographic projection corresponds to "and" view, where the components intersect each other to return the whole set. For example, a single coin toss can give head or tail, and one of the two options excludes the other, however, the whole that give heads and the whole that give tails are not alternative, but they intersect themselves to return the overall idea of coin toss.
Below we can see the metaphorical representation of an extended in space object. You remember the extended ones as characterized by an X element extraneous/overall to elements of logical disjunction, added to logical conjunction. The resulting Venn diagram corresponds to a strange three-dimensional shape, so we name “junction”. The extraneous/overall element seems a nail into the shape to fix the parts together.