Le Storie di Leo - Incrementare la produzione

E' un pomeriggio come tanti altri, quando Leo scende in strada per giocare con i suoi amici. Stranamente l'unico amico che incontra è Andrea, tutti gli altri non ci sono. "Hey Leo, pensa che ci sono fabbriche dove lavorano come matti per produrre i componenti elettronici di questi telefoni" dice Andrea. "Già...ciononostante non riescono a coprire la domanda" risponde Leo

In quel pomeriggio così noioso Leo ed Andrea non si aspettavano di certo l'apparizione di un mostro !

Si tratta di una visione insolita, simile ad una creatura aliena.

Questa volta l'incontro è piuttosto ravvicinato, perchè non è una sagoma fugace sullo sfondo, nè un'ipotesi per sentito dire dagli amici, ma una presenza ostile che richiede la ricerca immediata di una via di fuga.

E' un copione già visto.

Un mostro che li insegue e loro che devono fuggire.

E quel palazzo in costruzione, solido e grigio come l'atmosfera circostante, sarà il loro ultimo rifugio.

Leo non avrebbe mai immaginato di trovare proprio lì il suo amico Gianni.

"Hey Gianni, ma tu stavi qui ? E lo sai che di fuori c'è un mostro ?"

"Leo, dobbiamo sbrigarci a montare le lavatrici...siamo in ritardo con la produzione" risponde Gianni. "Ma queste lavatrici sono così importanti ?" domanda Leo. Gianni risponde:"Devi capire che si tratta di modelli originali. Sono assemblati con elementi scomponibili. Il problema principale delle vecchie lavatrici è che gli utenti non sapevano dove mettere le mani. Quando c'era un guasto dovevano per forza comprarne una nuova. Invece adesso basta sostituire un componente reperibile presso qualsiasi esercizio commerciale"

"Capisco" risponde Leo.

I due ragazzi salgono le scale al buio, attenti a non incespicare, finchè non raggiungono il secondo piano, ancora vuoto e senza illuminazione.

"Leo, vieni a vedere !!!" esclama Andrea.

Attraverso la fessura di una parete, che in futuro diventerà una finestra, si scorge il mostro che si aggira tra le case. "E' sempre lì ! Non possiamo uscire !" dice Andrea. Ma la quiete del secondo piano viene presto interrotta dai passi rumorosi e dal vociferare di un nuovo gruppo di lavoro che sta per insediarsi. Tra questi operai ci sono altri bambini della loro stessa età che vogliono guadagnarsi la paghetta, o anche solamente aiutare i loro genitori nel doposcuola.

"Marta, lo sai che qui fuori c'è un mostro ?" domanda Leo, sorpreso di incontrare la sua compagna di classe. 

"Papà, secondo te queste stoffe vanno bene ?" chiede Marta rivolgendosi al padre "Sì Marta, ma sbrigati. Ci sono venti scatoloni pieni" le risponde il padre.

"Uhmmm... al piano di sotto le lavatrici, e qui una sartoria !" riflette Andrea.

"Ma come fate a lavorare al buio ? Con il chiasso delle lavatrici ? E riuscite a concentrarvi ?" domanda Leo. "Certo !" risponde Marta mentre tira la stoffa con le mani "Non possiamo aspettare che mettano la corrente elettrica, ci basta la luce che viene da fuori"

Nel trambusto generale, tra il chiasso delle lavatrici e gli operai della sartoria, Leo e Andrea tornano allo scorcio sulla parete, ma ormai nulla è più come prima. Nel breve lasso di tempo in cui si sono allontanati, la visuale è stata coperta dalle vetrate di un palazzo. Fino a pochi istanti prima c'erano solo le basse fondamenta in cemento armato, ma in dieci minuti gli operai hanno installato le vetrate che adesso nascondono tutto il panorama circostante. Dove sarà il mostro ? Ormai non ha più spazio per muoversi.

"Ragazzini andatevene, che dobbiamo lavorare !" intima il padre di Marta.

I due ragazzi si convincono che non possono rimanere, storditi come sono dal rumore delle macchine per cucire e delle lavatrici. "E' incredibile ! Sembra che per tutte queste persone il mostro non significhi nulla ! Non se ne curano proprio" osserva Leo. Andrea ci pensa un pò e poi risponde sorridendo:

"Vedi Leo, forse nella società in cui viviamo non c'è più posto per i mostri.

Un mostro ha bisogno di tempo: prima di tutto c'è bisogno di qualcuno che si accorga di lui, che si soffermi ad osservarlo, e già questo è molto difficile, dato che tutti sono indaffaratissimi. Dopodichè è necessario porsi le domande giuste, capire da dove viene, che cosa vuole, ma i problemi della gente oggi sono altri."

"Hai proprio ragione" risponde Leo "In una società dove tutti studiano e lavorano non c'è posto per i mostri. Incrementare la produzione, raggiungere i propri obiettivi. Ecco, questo è' il modo migliore per tenerli lontani. Addio MOSTRO !!!"

Fine

Storia e disegni di Leo001

What is the secret of space extent ?

 “Geometry don’t teaches about description of lines and circles, but postulates it. Geometry requires that you already know how to describe these concepts; after, teaches how problems are solved by operations. Therefore, describing the line and the circle are not geometric problems.” 

(Philosophiæ Naturalis Principia Mathematica – Isaac Newton)

This post is dedicated to a very interesting topic:
for the first time we try to explain the space extent in logical-mathematical terms, to distinguish unextended elements, such numbers or variables, from extended in space elements, such geometric shapes.
Unextended ones are abstract, such as qualities, thoughts or concepts, and they haven’t height, width or depth.
Extended ones are material, such points, shapes, pictures, so they have height, width or depth.
In everyday life it means how to distinguish abstract concepts, such beauty, justice, happiness, length, color, and so on, from material objects, extended in space, such shapes, crystals, planets, animals and people. 
Space extent, as points, segments, triangles, solids, and so on, until now was intended for an axiom, or a "perception", but we can see below that can be understood as a particular logic structure. 
The ability to distinguish extended from unextended ones is innate and instinctive in human beings, extremely difficult to machines, computers and a.i., and until now had never been found a rational criterion. 

Before now, mathematics tried to distinguish discrete from continous, but they dont’care about more important and generic problem of distinguish extended from unextended, where discrete and continuous only are extended specific cases.
Neither Propositional Logic take care about that, because Propositional Logic, First and Second Order, puts extended elements into variables "x" and unextended elements in properties "F" referred to "x", “x -> Fx”, without explain difference between them.

Extended and unextended

Now we begin introducing a discursive criterion, and after, will continue with a rigorous definition. First of all, we can highlight a characteristic that distinguishes unextended from extended ones: the first are homogeneous, the second are heterogeneous, because extended ones possess overall qualities independent of their content. 

Let's start with some examples of unextended ones.

The number 2 is unextended idea, abstract, with no height, width or depth, and in fact it is homogeneous: it can only refer to objects that participate idea of 2, such two apples, two oranges, two eyes, but not to a single eye or a single apple, because they don’t participate the idea of 2.

Justice is unextended idea, abstract, with no height, width or depth, and in fact it is homogeneous: it can only refer to objects that participate the idea of justice, that is, policemen, judges, heroes and so on, but not an apple or a leg, because apples and legs have nothing to do with idea of justice.

Let’s start now with extended ones.

Triangle is extended, with height and width, and heterogeneous: contains points, sides or a circle inscribed in, but overall it can refer to qualities that have nothing to do with elements contained within. In fact, triangle can refer to Egyptian pyramids, road signs, love affairs, and many other concepts that are relevant to overall idea of a triangle but not to elements contained within.

A human being is extended, with height, width and depth, and heterogeneous: contains protons, neutrons and electrons, but overall it can refer to qualities that have nothing to do with elements contained within. It can refer to beauty, intelligence, ability to love, nourish and many other concepts that are relevant to overall idea of human being but not to elements contained within.

A typical example about difference between unextended and extended objects is difference between beauty and Miss America. 

Beauty is unextended and homogeneous: it can only refer to concepts that participate the idea of beauty, such harmony, youth, competitions, dances, and so on, but not to dental fillings, because they have nothing to do with idea of beauty. Opposite to beauty, Miss America is extended and heterogeneous: she contains bones, muscles and dental fillings, but overall it can refer to concepts of humanity and beauty. 

Another interesting example is difference between sunset and atmosphere.

Sunset is unextended and homogeneous: it can only refer to objects that participate the idea of sunset, as the Sun, clouds, landscape and the horizon, but not hydrogen and nitrogen, because they have nothing to do with idea of sunset. Opposite to sunset, atmosphere is extended and heterogeneous: it contains hydrogen and nitrogen, however can refer to Sun, clouds, landscape, the horizon and all those concepts that are relevant to overall idea of atmosphere.

Through all these examples the extended objects results ambivalent, because they have overall elements extraneous to their content.

How can we logically describe this concept?

First of all, let's start by defining what means "overall".

An object can be defined through a series of "or" conditions, that is logical disjunctions, to define its different manner, and its overall vision corresponds to a series of "and" conditions, that is logical conjunctions, where indissolubly binds manner together, in a single whole. Eg:

C = H or T

N(C) = N(H) and N(T)

This means coin tosses, "C", returns heads or tails, "H or T", however the set of all tosses, "N(C)", corresponds to the tosses that give heads, plus tails, “N(H) and N(T)”.

The function N(x) means "grouping of x", or "set of x", and is necessary otherwise the logical conjunction would return the empty set, since the single options are alternatives to each other, that is: " H and T = empty set ".

The function N(x) does not refer to a specific multiplicity, it is not certain that the single objects must be more than one. In the previous example, the coin tosses can be infinite, but in other cases the multiplicity is only one. In the next example we see a hand can be the right or the left, so the set of all hands is given by the right plus the left, with the multiplicities that are respectively two, one and one.

hand = right or left

N(hand) = N(right) and N(left)

Furthermore, the "and" conditions requires the objects inextricably linked in the overall ensemble, so that, by eliminating a single option, the whole set is invalid.

For example, a single hand can be the right, and not the left, but the overall set must necessarily contain both the right and the left. Similarly, the set of coin tosses must contain both tosses that give heads and those that give tails, even if, by chance, one of the two cases never occurs. Previous two examples referred to unextended objects, with no height, width or depth. Coin tosses are unextended events, because they are a concept with no space extent. In the same way, set of hands is unextended, because has no height, width or depth, although their single members, hands, are extended. In fact, you can see that an unextended object, such a set, can be composite by extended members: look at the set of the horses, is unextended, when the horses are extended. 

Let us now turn to extended objects.

We said extended objects are ambivalent, because they have overall parts that are extraneous to their content. This concept can be explained by next two expressions:

A = B1 or B2 or… or Bn

N(A) = N(B1) and N(B2) and … and N(Bn) and X

In the first expression we can see the component A in "n" different ways, as we have previously seen in the case of coin tosses or hands. In the second expression, we see the set of these elements, N(A), containing an extraneous/overall part "X", that is not related to elements of first expression, and appears only in logical conjunction. In other words, extended objects involve the breaking of the one-to-one correspondence between elements in logical disjunction and logical conjunction, which instead characterized unextended objects, with the addition of an extraneous element "X" in the logical conjunction.

Let's see some examples.

The next image depicts a square.

The square can be described by the next two expressions:

T = T1 or T2 or T3 or T4

Square = N(T) = N(T1) and N(T2) and N(T3) and N(T4) and X

The first expression means that the generic T element that composes the square can be the triangle T1 or T2 or T3 or T4. The second expression means that the square, in addition to containing the set of T elements, must have an X component, extraneous/overall to the individual elements, that could specifically indicate:

X = "has all sides equal", otherwise it would not be a square.

X is a property of N(T), just like the individual N(Tj).

Instead of X = "has all sides equal", we can write X = "has the elements one below the other", or X = "has the elements next to each other", and still we have extended in space objects, even if no squares, as you can see in the next picture. Only the lack of  X makes the unextended object, with no height, width or depth, reducing it to an abstract list of triangles, without space extent.

Let's see other examples of extended in space objects.

Look at the next picture, corresponding to a cabinet with two drawers and the base.

The cabinet can be described using the next two expressions:

C = a1 or … or an or b1 or … or bn or c1 or … or cn

Cabinet = N(C) = N(aj) and N(bj) and N(cj) and X

The first expression will means that the generic C element of the cabinet is a generic aj member of the first drawer, or a generic bj member of the second drawer, or a generic cj member of the base. The second expression means that the cabinet, in addition to containing the set of the two drawers and the base, has an X component, extraneous/overall to individual elements, to indicate that the two drawers and the base are placed one under the other, X = "one under the other". Otherwise the drawers and the base would not be connected in space extent.

Look at the next picture, corresponding to set of points B1, B2, B3 and B4.

Set of points B1, B2, B3, B4 can be described by next two expressions:

A = B1 or B2 or B3 or B4

N(A) = N(B1) and N(B2) and N(B3) and N(B4) and X

The first expression means that the generic point A is equal to B1 or B2 or B3 or B4. The second expression means that N(A), set of those points, in addition to have the Bn individual points, must have an X element, extraneous/overall to individual, to indicate X = "equidistant from C point”, otherwise it would be abstract,  not a material set of points extended on a plane. 

Instead of write X = "equidistant from C point”, we can write X = "equidistant from each other", and still we have a set of points extended in space. Only the lack of  X  makes an unextended set, without space extent.

The next examples are specifically about Mathematics.

A set of numbers, finite or infinite, is unextended in space, with no height, width or depth, and we can write it as:

I = {1, 2, 3, 4 ,… }

With our methodology, we can rewrite the set using the next two expressions:

n = 1 or 2 or 3 or 4 or …

N(n) = N(1) and N(2) and N(3) and N(4) and …

The first expression means that the generic element “n” is equal to 1 or 2 or 3 or 4 and so on. The second expression means that the set of those numbers is equal to 1 and 2 and 3 and 4 and so on. Now let's try to add an X element in logical conjunction, extraneous/overall to elements, such as X = "increasing order":

N (n) = N (1) and N (2) and N (3) and N (4) and… and X.

Well, we see that adding extraneous/overall X="increasing order", the unextended set becomes extended in space,  because “increasing order” means a straight line, a thermometer, a clock, which are all extended in space objects. In fact, the increasing order leads a position from bottom to top, or left to right, which are concepts inherent the space extent.

Let's see the next example.

“P” point in the “n” dimensional Cartesian space can be written as P = (x1, x2, x3,…, xn).

With our methodology, that point can be described by next two expressions:

r = x1 or x2 or x3 or … or xn

P = N(r) = N(x1) and N(x2) and N(x3) and … and N(xn) and X

The first identifies a generic real number "r", equal to x1 or x2 or x3 or… or xn. The second identifies “P” point, having in addition to real numbers an X element extraneous/overall to individual numbers, to indicate "numbers are coordinates", otherwise P would be only an abstract list of "n" real numbers. This X element characterizes P extended in space, such as the mathematical functions. Otherwise, the lack of X, reduce P to an unextended list of numbers.

Finally, we will conclude this paragraph giving one of the previous examples: 

difference between beauty, unextended in space, and Miss America, extended in space.

Beauty can be described by next two expressions:

example = harmony or youth or seduction

Beauty = N(example) = N(harmony) and N(youth) and N(seduction)

The first expression identifies a single example of beauty, equal to harmony, youth or seduction. The second expression defines beauty as the set of these singular examples, where the "or" elements are in perfect one-to-one correspondence with the "and" elements, without X extraneous/overall parts.

Opposite to beauty, Miss America can be described using next two expressions:

Element = bone or muscle or dental filling

Miss America = N(Element) = N(bone) and N(muscle) and N(dental filling) and X

The first expression identifies the generic component of Miss America as a bone, a muscle or a dental filling. The second expression identifies Miss America, having in addition to singular elements, an X component, extraneous/overall to singular elements, that means the beauty, harmony and seduction, to characterize whole set “Miss America” extended in space.

Three-dimensional Venn diagrams

The previous two paragraphs lead us to imagine concepts as two-faced objects. Each object has two faces: it can be a single element or a whole, depending on choose "or" or "and" operator. As you can see in the next picture, the metaphorical representation of an object is a three-dimensional Venn diagram. One of the two orthographic projections corresponds to "or" view, where the components are mutually exclusive and their intersection returns the empty set. The other orthographic projection corresponds to "and" view, where the components intersect each other to return the whole set. For example, a single coin toss can give head or tail, and one of the two options excludes the other, however, the whole that give heads and the whole that give tails are not alternative, but they intersect themselves to return the overall idea of coin toss.

Below we can see the metaphorical representation of an extended in space object. You remember the extended ones as characterized by an X element extraneous/overall to elements of logical disjunction, added to logical conjunction. The resulting Venn diagram corresponds to a strange three-dimensional shape, so we name “junction”. The extraneous/overall element seems a nail into the shape to fix the parts together.

The book

Lately, the author published the book "L’estensione nello spazio" (Space extent in english), edited by YouCanPrint, January 2022, where for the first time defines space extent with these concepts. The book explains other important issues, such as difference between abstract and concrete,  potentiality and actuality, spacetime, using the same Kantian criterion of analytic and synthetic propositions. New edition of the book will be released shortly, containing revisions, improvements, and references to Propositional Logic and three-dimensional Venn diagrams that you have seen here.

il segreto dell'estensione nello spazio

 “La Geometria non insegna la descrizione delle linee rette e dei circoli, ma la postula. Richiede che, prima di pervenire ai suoi ammaestramenti, si sappiano già descrivere; dopodiché insegna come si risolvono dei problemi per mezzo di tali operazioni. Perciò, descrivere la retta ed il circolo non sono problemi geometrici. (Principi di Filosofia Naturale di Isaac Newton)

Questo post è dedicato ad un argomento molto interessante:

per la prima volta si vuole spiegare l’estensione nello spazio in termini logico-matematici, cioè, distinguere un elemento incorporeo, come un numero o una variabile, da un elemento corporeo, spazialmente esteso, come una figura geometrica.

Nella vita di tutti i giorni si traduce nella possibilità di distinguere logicamente concetti astratti, come la bellezza, la giustizia, la felicità, la lunghezza, il colore, e via dicendo, da oggetti materiali, estesi nello spazio, come figure geometriche, cristalli, pianeti, animali e persone. L’estensione nello spazio, cioè l’esistenza di punti sul piano, segmenti, triangoli, solidi, e via dicendo, è sempre stata posta come assioma, o come “percezione sensibile”, ma di seguito vedremo che può ricondursi ad una particolare struttura logica. La capacità di distinguere il corporeo dall’incorporeo è innata ed istintiva negli esseri umani, difficilissima per le macchine, e  finora non si era mai trovato un criterio razionale per definirla.

Fino ad oggi la matematica ha tentato di distinguere il discreto dal continuo, ma non si è mai occupata del problema molto più importante e generico di distinguere l’incorporeo dal corporeo, laddove il discreto e il continuo sono solamente casi specifici del corporeo.

Tanto meno si è occupata di questo problema la logica, che ha sempre posizionato elementi corporei tra le variabili proposizionali generiche “x” ed elementi incorporei tra le proprietà “F” attribuibili ad “x”,  x-->Fx, senza mai spiegare in cosa consista la differenza tra loro.

Corporeo ed incorporeo

Iniziamo con un criterio discorsivo, dopodichè si proseguirà con una definizione rigorosa. Innanzitutto possiamo evidenziare una caratteristica che distingue gli oggetti incorporei da quelli corporei: i primi sono omogenei, mentre i secondi sono eterogenei, in quanto possiedono qualità complessive indipendenti dal loro contenuto. Iniziamo con alcuni esempi di oggetti incorporei.

Il numero 2 è incorporeo e infatti è omogeneo: può riferirsi solamente ad oggetti che partecipano della sua idea di 2, come due mele, due arance, due occhi, però non a un singolo occhio o a una singola mela, perché questi ultimi non partecipano della sua idea di 2.

La giustizia è un'idea incorporea e infatti è omogenea: può riferirsi solamente a oggetti che partecipano dell'idea di giustizia, cioè i poliziotti, i magistrati, gli eroi e via dicendo, ma non a una mela o a una gamba, perché la mela e la gamba non hanno niente a che fare con l'idea di giustizia.

Passiamo adesso agli oggetti corporei.

il triangolo è corporeo e infatti è eterogeneo: può contenere punti, cateti e un cerchio inscritto in esso, ma complessivamente può riferirsi a delle qualità che non hanno niente a che fare con gli elementi contenuti al suo interno. Infatti può riferirsi alle piramidi egizie, alle segnaletiche stradali, ai rapporti amorosi, e a tanti altri concetti che sono attinenti all’idea complessiva di triangolo ma non agli elementi contenuti al suo interno. 

Un essere umano è corporeo e infatti è eterogeneo: contiene protoni, neutroni ed elettroni, ma complessivamente può riferirsi a delle qualità che non hanno niente a che fare con gli elementi contenuti al suo interno. Infatti può riferirsi alla bellezza, all’intelligenza, alla capacità di amare, nutrirsi e a tanti altri concetti che sono attinenti all’idea complessiva di umano ma non agli elementi contenuti al suo interno.

Un tipico esempio di differenza tra oggetto incorporeo e corporeo è la differenza tra la bellezza e Miss Italia. La bellezza è incorporea e infatti è omogenea: può riferirsi solamente a concetti che partecipano dell’idea di bellezza, come l’armonia, la giovinezza, i concorsi, i balli, e via dicendo, ma non alle otturazioni dentali, perché queste ultime non hanno niente a che fare con l’idea di bellezza. Al contrario, Miss Italia è corporea e infatti è eterogenea: contiene ossa, muscoli e otturazioni dentali, ma complessivamente può riferirsi a quei concetti complessivi di umanità e bellezza.

Un altro esempio interessante è la differenza tra il tramonto e l’atmosfera.

Il tramonto è un’idea incorporea e infatti è omogeneo: può riferirsi solamente a oggetti che partecipano dell’idea di tramonto, come il Sole, le nuvole, il panorama e l’orizzonte, ma non all’idrogeno e all’azoto, perchè questi ultimi non hanno niente a che fare con l’idea di tramonto. Al contrario l’atmosfera è corporea e infatti è eterogenea: contiene idrogeno e azoto, ma al tempo stesso può riferirsi al Sole, alle nuvole, al panorama, all’orizzonte e a tutti quei concetti che sono attinenti all’idea complessiva di atmosfera.

Tramite tutti questi esempi abbiamo visto che gli oggetti corporei sono ambigui, perché contengono elementi complessivi non pertinenti al loro contenuto.

Come possiamo descrivere in termini logici questo concetto ?

Innanzitutto iniziamo col definire cosa si intende per “complessivo”.

Un singolo oggetto può essere definito tramite una serie di condizioni “or”, cioè di somme logiche, che caratterizzano i suoi diversi modi di essere, mentre la sua visione complessiva corrisponde ad una serie di relazioni “and”, cioè ad un prodotto logico, che lega indissolubilmente tra loro, in un unico insieme, quei diversi modi di essere. Ad esempio:

L = T or C

N(L) = N(T) and N(C)

Con questa espressione diciamo che il singolo lancio di una moneta, “L”, restituisce testa o croce, “T or C”, mentre l’insieme di tutti i lanci della moneta, “N(L)”, corrisponde ai lanci che danno testa, più i lanci che danno croce, “N(T) and N(C)”.

La funzione N(x) può significare “raggruppamento di x”, oppure “insieme di x”, e si rende necessaria perché altrimenti il prodotto logico restituirebbe l’insieme vuoto, dal momento che le singole opzioni sono alternative tra loro, cioè: “T and C = insieme vuoto”.

La funzione N(x) non si riferisce ad una molteplicità specifica, non è detto che i singoli oggetti debbano essere più di uno. Nell’esempio precedente i lanci di una moneta possono essere infiniti, ma in altri casi la molteplicità è solamente uno. Nel prossimo esempio vediamo che una mano può essere la destra o la sinistra, quindi l’insieme di tutte le mani è dato dalla destra più la sinistra, con le molteplicità che sono rispettivamente due, uno ed uno.

mano = destra or sinistra

N(mano) = N(destra) and N(sinistra)

Inoltre, si noti che le condizioni “and” richiedono che gli oggetti siano legati indissolubilmente nell’insieme complessivo, per cui, eliminando anche una sola opzione, tutto l’insieme risulta non valido.

Ad esempio, una singola mano può essere la destra, e non la sinistra, ma l’insieme complessivo deve contenere necessariamente sia la destra che la sinistra. Allo stesso modo, l’insieme di tutti i lanci di una moneta deve contenere sia i lanci che danno testa, che quelli che danno croce, anche se, casualmente, uno dei due casi non si verifica mai.

I due esempi visti finora si riferivano ad oggetti incorporei. 

I lanci di una moneta sono eventi incorporei, perché non hanno estensione spaziale. Allo stesso modo l’insieme delle mani è incorporeo, non ha estensione spaziale, perché si tratta solamente di un concetto, anche se gli elementi di quest’ultimo insieme, cioè le singole mani, sono corporee. 

Si noti infatti che un oggetto incorporeo può essere costituito da elementi corporei: l’insieme dei cavalli è incorporeo, non ha altezza, larghezza e spessore, ciononostante i singoli cavalli lo hanno.

Idem per l’insieme delle patate o degli alunni di una classe.

Passiamo adesso agli oggetti corporei.

Avevamo detto che gli oggetti corporei sono ambigui, perché hanno parti complessive estranee al loro contenuto. Questo concetto può essere riassunto tramite le seguenti due espressioni:

A = B1 or B2 or… or Bn

N(A) = N(B1) and N(B2) and … and N(Bn) and X

Nella prima espressione vediamo che il singolo componente A può essere in “n” modi diversi, come abbiamo già visto precedentemente nel caso dei singoli lanci delle monete o delle singole mani.

Nella seconda espressione invece, vediamo che l’insieme complessivo di questi elementi, N(A), contiene una parte estranea/complessiva “X”, che non è afferente agli elementi della prima espressione, e che appare solamente nel prodotto logico. In altre parole, gli oggetti corporei comportano la rottura della corrispondenza biunivoca tra elementi in somma logica ed elementi in prodotto logico, che invece caratterizzava gli oggetti incorporei, con l’aggiunta di un elemento estraneo “X” nel prodotto logico.

Vediamo alcuni esempi.

La prossima immagine raffigura un quadrato.

Il quadrato può essere descritto tramite le seguenti due espressioni:

T = T1 or T2 or T3 or T4

Quadrato = N(T) = N(T1) and N(T2) and N(T3) and N(T4) and X

La prima espressione significa che il generico elemento T che lo compone può essere il triangolo T1 or T2 or T3 or T4. La seconda espressione significa che il quadrato, oltre a contenere l’insieme degli elementi T, deve avere un componente X, estraneo/complessivo ai singoli elementi, che nello specifico potrebbe indicare: 

X = “ha tutti i lati uguali”, altrimenti non sarebbe un quadrato.

Quindi X è una proprietà di N(T), esattamente come i singoli N(Tj).

Si noti che se invece di scrivere X="ha tutti i lati uguali", avessimo scritto X="ha gli elementi uno sotto l'altro", oppure X="ha gli elementi uno accanto all'altro", avremmo ancora ottenuto oggetti corporei estesi nello spazio, come si deduce dalla prossima immagine. E’ solamente la mancanza dell'elemento X che rende l'oggetto incorporeo, riducendolo ad una lista astratta di triangoli, senza estensione spaziale.

Vediamo altri esempi di oggetti corporei.

Osservate la figura seguente, corrispondente ad un mobile con due cassetti e la base.

Il mobile può essere descritto tramite le seguenti due espressioni:

M = a1 or … or an or b1 or … or bn or c1 or … or cn

Mobile = N(M) = N(aj) and N(bj) and N(cj) and X

La prima espressione significa che il generico elemento M che lo compone può essere un generico componente aj del primo cassetto, oppure un generico componente bj del secondo cassetto, oppure un generico componente cj della base. La seconda espressione significa che il mobile, oltre a contenere l’insieme dei due cassetti e della base, deve avere un componente X, estraneo/complessivo ai singoli elementi, che sta ad indicare che i due cassetti e la base sono messi uno sotto l’altro, X = “uno sotto l’altro”. Altrimenti i cassetti e la base non sarebbero connessi nello spazio.

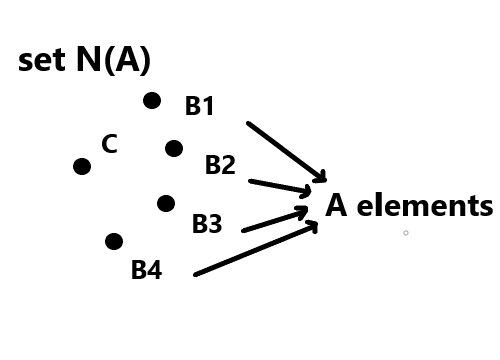
Osservate la figura seguente, corrispondente all’insieme dei punti B1, B2, B3 e B4.

L’insieme dei punti B1, B2, B3, B4 può essere descritto tramite le seguenti due espressioni:

A = B1 or B2 or B3 or B4

N(A) = N(B1) and N(B2) and N(B3) and N(B4) and X

La prima espressione significa che il generico punto A può essere B1 or B2 or B3 or B4. La seconda espressione significa che l’insieme N(A) di quei punti, oltre a contenere i singoli punti Bn, deve contenere un elemento X, estraneo/complessivo ai singoli elementi, che sta ad indicare X = “equidistanti dal punto C”, altrimenti sarebbe un insieme astratto e non un insieme corporeo di punti sul piano.

Si noti che se invece di scrivere X=" equidistanti dal punto C ", avessimo scritto X="equidistanti tra loro", avremmo ancora ottenuto un insieme corporeo di punti sul piano. E’ solamente la mancanza dell'elemento X che rende l'insieme astratto e incorporeo, senza estensione spaziale.

I prossimi esempi riguardano nello specifico la matematica.

Un insieme di numeri, finito o infinito, è incorporeo, non ha estensione spaziale, e possiamo scriverlo come:

I = {1, 2, 3, 4 ,… }

Con il nostro procedimento, quell’insieme può essere descritto tramite le seguenti due espressioni:

n = 1 or 2 or 3 or 4 or …

N(n) = N(1) and N(2) and N(3) and N(4) and …

La prima espressione significa che il generico elemento n che lo compone può essere il numero 1 o il 2 o il 3 o il 4 e così via. La seconda espressione significa che l’insieme di quei numeri contiene 1 e 2 e 3 e 4 e così via.

Adesso proviamo ad aggiungere un elemento X nel prodotto logico, estraneo/complessivo ai singoli elementi, ad esempio X=”ordine crescente”, come di seguito: N(n) = N(1) and N(2) and N(3) and N(4) and … and X.

Ebbene, vediamo che aggiungendo l’elemento estraneo/complessivo X dell’ordine crescente quell’insieme incorporeo è diventato corporeo, perché i numeri in ordine crescente possono essere disposti su una retta, un termometro, un orologio, che guarda caso sono tutti oggetti corporei estesi nello spazio. Infatti l’ordine crescente presuppone un orientamento dal basso verso l’alto, o da sinistra verso destra, che sono tutti concetti inerenti l’estensione nello spazio.

Vediamo l’esempio seguente.

Un punto P dello spazio cartesiano ad “n” dimensioni può essere scritto come P=(x1,x2,x3,…,xn).

Con il nostro procedimento, quel punto può essere descritto tramite le seguenti due espressioni:

r = x1 or x2 or x3 or … or xn

P = N(r) = N(x1) and N(x2) and N(x3) and … and N(xn) and X

La prima espressione identifica un generico numero reale “r”, che può essere x1 or x2 or x3 or … or xn.

La seconda espressione identifica il punto P, che oltre a contenere i singoli numeri reali “r”, deve avere un componente X, estraneo/complessivo ai singoli numeri, che sta ad indicare che “i numeri sono coordinate nello spazio”, altrimenti sarebbe solamente un insieme astratto di “n” numeri. Questo elemento X caratterizza il punto nello spazio come un oggetto corporeo, dal che ne risulta che tutti gli oggetti dello spazio cartesiano, come le funzioni matematiche, sono corporei, cioè estesi nello spazio. La mancanza di X, invece, degrada il punto ad un’insieme incorporeo di numeri reali.

Infine, chiudiamo questo paragrafo riprendendo uno degli esempi precedenti, quello sulla differenza tra la bellezza, che è incorporea, e Miss Italia, che è corporea.

La bellezza può essere descritta tramite le seguenti due espressioni:

esempio = armonia or gioventù or seduzione

Bellezza = N(esempio) = N(armonia) and N(gioventù) and N(seduzione)

La prima espressione identifica un singolo esempio di bellezza, che può essere l’armonia, la gioventù o la seduzione. La seconda espressione caratterizza la bellezza come l’insieme di tutti questi singoli esempi, dove gli elementi “or” sono in perfetta corrispondenza biunivoca con gli elementi “and”, senza nessuna parte estranea/complessiva X.

Invece Miss Italia può essere descritta tramite le seguenti due espressioni:

Elemento = osso or muscolo or otturazione dentale

Miss Italia = N(Elemento) = N(osso) and N(muscolo) and N(otturazione dentale) and X

La prima espressione significa che il generico elemento che compone Miss Italia può essere un osso, un muscolo o un’otturazione dentale. La seconda espressione significa che Miss Italia, oltre a contenere l’insieme di quegli elementi,  deve avere un componente X, estraneo/complessivo ai singoli elementi, che sta proprio a significare la bellezza, l’armonia e la seduzione, che caratterizzano complessivamente Miss Italia.

Diagrammi tridimensionali di Eulero-Venn

I due paragrafi precedenti consentono di immaginare gli oggetti del nostro pensiero in maniera duale. Ogni oggetto ha una doppia faccia: può essere visto come singolo elemento o come insieme, a seconda che si scelga di utilizzare l'operatore "or" oppure "and". Come possiamo vedere dalla prossima immagine, questa doppia faccia di uno stesso oggetto comporta la sua raffigurazione metaforica tramite un diagramma di Eulero-Venn tridimensionale. Una delle due proiezioni ortogonali corrisponde alla visione "or", dove i componenti sono vicendevolmente esclusivi e la loro intersezione restituisce l'insieme vuoto. L'altra proiezione ortogonale corrisponde alla visione "and", dove i componenti si intersecano tra loro per restituire l'insieme complessivo. Ad esempio, il singolo lancio di una moneta può dare testa o croce, e una delle due opzioni esclude l'altra, però, l'insieme dei lanci che danno testa e di quelli che danno croce non si escludono, ma si intersecano per restituire l'idea complessiva di lancio.

Di seguito vediamo la raffigurazione metaforica di un oggetto corporeo, esteso nello spazio.

Ricordiamo che gli oggetti corporei sono caratterizzati dalla presenza di un elemento X estraneo/complessivo agli elementi in somma logica, che va ad aggiungersi nel prodotto logico. Il diagramma di Eulero-Venn che ne risulta corrisponde ad una strana figura tridimensionale, che potremmo chiamare “giunzione”. L’elemento estraneo/complessivo sembra un chiodo che penetra la figura tridimensionale per tenerne unite le parti.

 

Il libro

Attualmente l’autore ha pubblicato il libro “L’estensione nello spazio”, edito da YouCanPrint nel gennaio 2022, che per la prima volta definisce la corporeità e l’estensione nello spazio sulla base di questi concetti. Nel libro vengono risolte altre questioni importanti, come la differenza tra astratto e concreto, il passaggio dalla potenza all’atto e lo spaziotempo, sempre avvalendosi di una medesima metodologia, basata sul criterio kantiano della distinzione tra giudizi analitici e sintetici. A breve uscirà una seconda edizione del libro contenente alcune migliorie, più i riferimenti alla Logica Proposizionale e ai diagrammi tridimensionali di Eulero-Venn che avete già letto qui.