Il mistero dei punti di fuga

Ragazzi, l’altro giorno in ufficio mi sono soffermato ad osservare il soffitto (non avevo proprio nulla da fare, direte voi, ma in quel momento no, ero in attesa di essere riassegnato ad altre mansioni).

Stavo contemplando la numerosità dei punti di fuga prospettici e l’immagine era talmente misteriosa e suggestiva che ho voluto fotografarla e riportarla qui.

Come potete notare, oltre al punto di fuga centrale, sul quale convergono le linee parallele che delimitano i fori sul soffitto, si vengono a creare tutta una molteplicità di altri punti di fuga, visibili soprattutto lateralmente a sinistra, a ridosso delle colonne.

Incuriosito e stupito da questo fatto, mi sono chiesto se esista una legge matematica che stabilisca la quantità di punti di fuga che una superficie debba avere.

La prospettiva deriva infatti dalla matematica e dalla geometria, e tutti noi a scuola abbiamo avuto almeno un’ora alla settimana dedicata allo studio del disegno tecnico.

Quindi mi sono messo a cercare su Wikipedia, dove ho trovato una trattazione molto estesa dello studio geometrico della prospettiva, risalente al periodo del Rinascimento, e proseguita poi in epoche successive.
Eppure, nonostante tutte queste trattazioni matematiche, non ho trovato una sola formula che permetta di stabilire quanti punti di fuga un oggetto debba avere.
Ho cercato anche altrove su internet, ma non ho trovato la risposta a questa mia domanda.

Esiste una legge matematica che stabilisca quanti punti di fuga una superficie debba avere ???

Perché un soffitto ha X punti di fuga, mentre un altro ne ha solo Y ???

Posso calcolare a priori quanti punti di fuga debba avere un soffitto, una superficie o un oggetto solido ???

Non trovando una risposta a queste mie domande, ho continuato ad osservare.

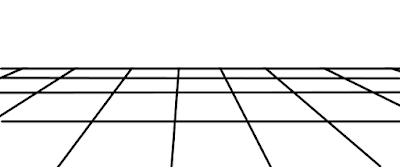
Nell’immagine sottostante, ho disegnato uno schema astratto di superficie reticolare, consistente in linee parallele e perpendicolari, dove si può notare un unico punto di fuga centrale.

L’immagine successiva mostra un’altra superficie reticolare, che sembra un pavimento vero, e qui possiamo notare che oltre al punto di fuga centrale se ne vedono altri due laterali, fuori campo, rispettivamente uno a destra e uno a sinistra.

Perché si vengono a creare più punti di fuga ?

Nello specifico, i due punti di fuga laterali sono quelli più “naturali”, perché derivano dalla presenza di linee oblique, mentre quello centrale è inspiegabile. A ben vedere, questo punto di fuga centrale, dipende da una proprietà delle mattonelle, per cui in lontananza, forse a causa della dispersione della luce, le mattonelle bianche sembrano più grandi di quelle nere, al punto che queste ultime si restringono fino a ridursi a righe sopra una superficie interamente bianca, con un loro punto di fuga centrale.
In questo caso quindi, la molteplicità dei punti di fuga dipende da proprietà specifiche della superficie osservata, non da una formula astratta a prescindere.

Ora, tornando all’immagine del soffitto dell’ufficio, anche qui possiamo notare come i diversi punti di fuga nascano da proprietà specifiche del soffitto, non da formule astratte a prescindere.

Esempi:
un primo punto di fuga è dovuto alle linee parallele che delimitano i buchi

un altro punto di fuga è dovuto alle scalanature all’interno dei fori, all'interno dei quali c'è una zona che rimane sempre in ombra, per cui tutte queste zone in ombra all’interno dei fori vengono a costituire una sequenza convergente.

      

      un altro punto di fuga scaturisce dalla dispersione della luce, come nell’esempio del pavimento, per cui andando verso la luce della finestra le scalanature nere appaiono più sottili fino a costituire linee nere con i loro specifici punti di fuga.

Da tutte queste considerazioni appare evidente il fatto che i punti di fuga non scaturiscono da una legge matematica a priori, cioè da un processo di astrazione, ma che al contrario, scaturiscono dalle proprietà particolari e contingenti dei singoli oggetti e delle superfici, cioè da un processo postumo di “concrezione”, al contrario dell’astrazione.

Il nostro occhio, o meglio il nostro cervello, distingue immediatamente, in un millisecondo, tutte queste numerose proprietà di un oggetto e ne individua i punti di fuga, laddove invece la nostra mente razionale impiega molto tempo a distinguere e a trovare una spiegazione.

Quindi non può esistere una legge matematica generale per il numero di punti di fuga, perché questo numero è determinato dalle situazioni di circostanza, come le scalanature, l’illuminazione, le decorazioni, gli accessori, e qualsiasi altro elemento contingente che si ripeta in serie nell’ambito della superficie.

Ogni oggetto possiede sue proprietà e caratteristiche specifiche, alcune delle quali si ripetono in serie, e sono proprio queste ultime a produrre i suoi punti di fuga, non una regola astratta.